Izrek o stranicah v pravokotnem trikotniku
Ana je načrtala pravokotni trikotnik s katetama, dolgima [latex]4\, \mathrm{cm}[/latex] in [latex]3\, \mathrm{cm}[/latex]. Izmerila je dolžino tretje stranice-hipotenuze. Zanimalo jo je, kako bi izračunala njeno dolžino.
Zanimivo je, da tretja stranica meri natanko [latex]5\, \mathrm{cm}[/latex]. Premišljevala je, ali je mogoče v pravokotnem trikotniku dolžine stranic tudi izračunati. Odgovor je dobila, ko je izvedela več o pravilu, ki velja med stranicami pravokotnega trikotnika.
Stranice v pravokotnem trikotniku
Hipotenuza je najdaljša stranica in leži nasproti pravemu kotu.
Kateti sta krajši stranici, ki oklepata pravi kot.
Mojster reši
Zgled 1
Spoznaj pravilo, ki velja med stranicami v pravokotnem trikotniku.
Grški matematik Pitagora je zapisal način in dokaz, kako izračunamo tretjo stranico pravokotnega trikotnika, če sta znani drugi dve. Nad vsako od stranic trikotnika načrtamo kvadrat. Obstaja povezava med ploščinami teh treh kvadratov.
Ploščina kvadrata nad hipotenuzo [latex]c[/latex] z dolžino [latex]5[/latex] enot je [latex]25\, \mathrm{e^2}[/latex].
Ploščina kvadrata nad kateto [latex]a[/latex] z dolžino [latex]4[/latex] enote je [latex]16\, \mathrm{e^2}[/latex].
Ploščina kvadrata nad kateto [latex]b[/latex] z dolžino [latex]3[/latex] enote je [latex]9\, \mathrm{e^2}[/latex].
Ko seštejemo ploščini kvadratov nad katetama, opazimo, da je vsota enaka ploščini kvadrata nad hipotenuzo.
Ugotovimo, da je [latex]25=16+9[/latex].
Če nadomestimo vrednosti za kateti in hipotenuzo z njihovimi oznakami, zapišemo zvezo med stranicami pravokotnega trikotnika: [latex]c^2=a^2+b^2[/latex].
Pitagorov izrek
V pravokotnem trikotniku je ploščina kvadrata nad hipotenuzo enaka vsoti ploščin kvadratov nad katetama.
[latex]h^2={k_1}^2+{k_2}^2[/latex]
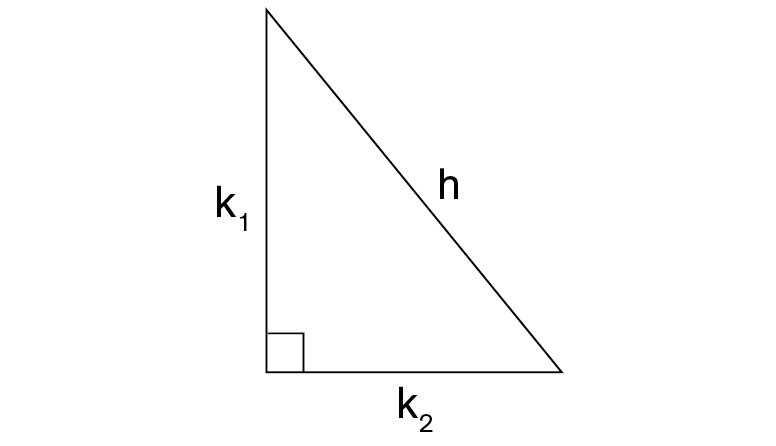
Pitagorov izrek uporabimo za računanje dolžin stranic v pravokotnem trikotniku.
Grški matematik Pitagora se je rodil leta
570 pr. n. št. na otoku Samosu v Grčiji in umrl 500 pr. n. št.
Zgled 2
Izračunaj hipotenuzo pravokotnega trikotnika s katetama [latex]a=8\, \mathrm{cm}[/latex] in [latex]b=6\, \mathrm{cm}[/latex].
Iz znane ploščine kvadrata nad stranico dobimo dolžino stranice s pomočjo kvadratnega korena ploščine kvadrata.
Ploščina kvadrata nad kateto [latex]a[/latex] je [latex]64\, \mathrm{cm^2}[/latex] in ploščina kvadrata nad kateto [latex]b[/latex] je [latex]36\, \mathrm{cm^2}[/latex].
Če seštejemo ploščini kvadratov nad katetama, dobimo:
[latex]a^2+b^2=[/latex]
[latex]=8^2+6^2=[/latex]
[latex]=64+36=[/latex]
[latex]=100[/latex]
Opazimo, da je vsota ploščin kvadratov nad katetama enaka ploščini kvadrata nad hipotenuzo.
[latex]c^2=100[/latex]
Stranico kvadrata nad hipotenuzo dobimo tako, da izračunamo kvadratni koren števila [latex]100[/latex].
[latex]c=\sqrt{100}[/latex]
[latex]c=10\, \mathrm{cm}[/latex]
Ugotovimo, da če sta znani dve stranici pravokotnega trikotnika, lahko izračunamo tretjo stranico.
V našem primeru meri hipotenuza [latex]10\, \mathrm{cm}[/latex].
Zgled 3
Pitagorov izrek ponazorimo s kvadrati nad stranicami pravokotnega trikotnika.
Ploščina kvadrata nad kateto je enaka razliki med
ploščino kvadrata nad hipotenuzo in
ploščino kvadrata nad drugo kateto.
[latex]\begin{aligned}a^2&=c^2-b^2 \\ b^2&=c^2-a^2 \end{aligned}[/latex]
Pri vseh nalogah lahko žepno računalo uporabiš za izračun kvadratov naravnih števil, večjih od [latex]20[/latex], in za izračun kvadratnih korenov, ki jih ne prepoznaš kot popolne kvadrate naravnih števil.