Površina valja
Luka želi iz kartona narediti model valja, ki bo visok [latex]4\, \mathrm{cm}[/latex] in širok [latex]3\, \mathrm{cm}[/latex]. Kakšne ploskve naj izreže?
Za izdelavo modela valja mora Luka izrezati dva enako velika kroga s polmerom [latex]1{,}5\, \mathrm{cm}[/latex], ki bosta osnovni ploskvi valja. Širina valja je namreč enaka premeru osnovne ploskve, zato je njen polmer [latex]1{,}5\, \mathrm{cm}[/latex].
Plašč ima obliko pravokotnika, ki ga zvijemo v tulec. Širina tega pravokotnika je enaka višini valja, to je [latex]4\, \mathrm{cm}[/latex]. Dolžina pravokotnika je enaka obsegu osnovne ploskve, to je [latex]o=2\pi\cdot r=2\pi\cdot1{,}5=3\pi[/latex], kar je približno [latex]9{,}4\, \mathrm{cm}[/latex]. Za računanje je Luka uporabil žepno računalo in za število [latex]\pi[/latex] pritisnil tipko [latex]\pi[/latex]. Tako je dobil dovolj točno vrednost dolžine, zaokroženo na milimetre, saj bolj natančno zaokroževanje ni smiselno.
Približka števila [latex]\pi[/latex]
[latex]\pi\doteq3{,}14[/latex]
[latex]\pi\doteq\frac{22}{7}[/latex]
Luka naj izreže dva skladna kroga s polmerom [latex]1{,}5\, \mathrm{cm}[/latex] ter pravokotnik, dolg [latex]9{,}4\, \mathrm{cm}[/latex] in širok [latex]4\, \mathrm{cm}[/latex].
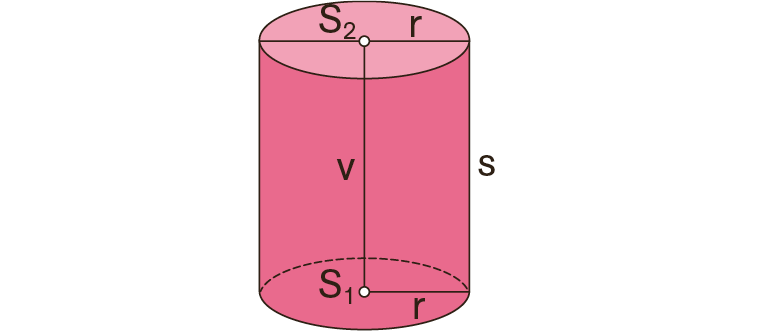
Valj je okroglo telo, ki ga omejujejo dva skladna in vzporedna kroga ter ena kriva ploskev.
Mojster reši
Zgled
Koliko kvadratnih centimetrov kartona potrebujemo za izdelavo [latex]4\,\mathrm{cm}[/latex] visokega in [latex]3\,\mathrm{cm}[/latex] širokega valja? ([latex]\pi\doteq 3{,}14[/latex])
Ker nas zanima, koliko kartona potrebujemo za izdelavo modela valja, bomo izračunali ploščine vseh mejnih ploskev, ki omejujejo valj, in jih sešteli.
[latex]P=2\cdot O+pl[/latex]
[latex]P=2\cdot\pi r^2+pl[/latex]
[latex]P=2\cdot\pi r^2+2\pi r\cdot v[/latex]
[latex]P=2\pi r(r+v)[/latex]
Površino valja sestavljajo dve osnovni ploskvi in plašč.
Ploščina ene osnovne ploskve, ki je krog, je [latex]O=\pi r^2[/latex].
Ploščina plašča je enaka ploščini pravokotnika z dolžino, ki je enaka obsegu kroga [latex]2\pi r[/latex], in širino, ki je enaka višini valja.
Izpostavimo faktor [latex]2\pi r[/latex]. Po tem obrazcu izračunamo površino valja.
Površina valja
[latex]P=2\cdot O+pl[/latex]
[latex]P=2\pi r(r+v)[/latex]
Ploščina osnovne ploskve valja
[latex]O=\pi r^2[/latex]
Ploščina plašča valja
[latex]pl=o\cdot v[/latex]
[latex]pl=2\pi r\cdot v=2\pi rv[/latex]
Valj
[latex]2r=3\, \mathrm{cm}[/latex]
[latex]\underline{v=4\, \mathrm{cm}}[/latex]
[latex]P=[/latex] ?
[latex]P=2\cdot O+pl[/latex]
[latex]P=2\cdot\pi r^2+2\pi r\cdot v[/latex]
[latex]P=2\pi r(r+v)[/latex]
[latex]P=2\pi\cdot1{,}5\cdot(1{,}5+4)[/latex]
[latex]P=3\pi\cdot5{,}5[/latex]
[latex]P=16{,}5\pi[/latex]
[latex]P\doteq 16{,}5 · 3{,}14[/latex]
[latex]P \doteq 51{,}81\, \mathrm{cm}^2[/latex]
Valj je pokončen, če je dolžina stranice valja enaka njegovi višini.
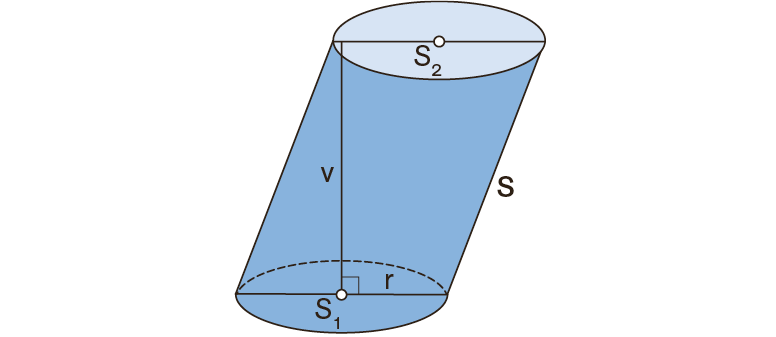
Pri poševnem valju stranski rob in višina valja nista enako dolga.
Vaja dela mojstra
Pri računanju lahko uporabiš žepno računalo.
Če so količine izražene s številom [latex]\pi[/latex], ga uporabimo tudi pri nadaljnem računanju in rezultat izrazimo z njim. Pravimo, da je rezultat točen.